Fonction dérivée
Cours / Activité à remplir avec le professeur.
I Tangente en un point, nombre dérivé
II Calcul de dérivées
III Lien entre la dérivée et les variations d'une fonction
IV Cas concret : Optimisation de bénéfices
Cours / Activité à remplir avec le professeur.
Objectifs pédagogiques :
- Utiliser les formules et les règles de dérivation pour déterminer la dérivée d’une fonction.
- Étudier, sur un intervalle donné, les variations d’une fonction à partir du calcul et de l’étude du signe de sa dérivée. Dresser son tableau de variation.
- Déterminer un extremum d’une fonction sur un intervalle donné à partir de son sens de variation.
I Tangente en un point, nombre dérivé
Considérons la fonction f définit par ]
1. Remplir le tableau de variation ci dessous.
Voici la courbe de la fonction
2. Déterminer la pente de la tangente aux point A, B et et C en complétant le tableau ci dessous.
CONCLUSION :
-
Le tableau de valeur obtenu est celui d'une fonction linéaire g définie par g(x) = ..............
-
Cette nouvelle fonction est appelée fonction dérivée de la fonction f. On la note f'.
-
f(x)= .............. f'(x)= ..............
-
La pente de la tangente en un point de la courbe, d'abscisse donnée, est appelée nombre dérivé de la fonction f
II Calcul de dérivées
Formulaire de dérivées :
Exercices d'entrainement :
III Lien entre la dérivée et les variations d'une fonction
1. Compléter le tableau ci dessous :
2. Calculer f'(x), la fonction dérivée de la fonction f(x).
3. Calculer :
-
f'(-4) = ......
-
f'(-1) = ......
-
f'(2) = ......
4. Compléter le tableau suivant :
Dérivées - Bilan
Soit f une fonction définie sur un intervalle I, et admettant une dérivée f' sur I.
Si, pour tout x de I, f'(x) > 0, alors est croissante sur I.
Si, pour tout x de I, f'(x) > 0, alors est décroissante sur I.
Si, pour tout x de I, f'(x) = 0, alors est constante sur I.
Une fonction atteint un extremum local ( maximum ou minimum ) lorsque f'(x) = 0.
En effet, dans l'étude de fonction réalisée en amont, nous pouvoir voir sur le tableau et sur la courbe, que la fonction atteint un minimum en x = -1.( sur l'intervalle On remarque aussi que f'(-1) = 0.







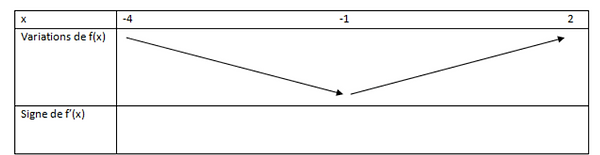
Soit la fonction f définie par f(x) =
Voici sa courbe représentative.
Application :
Soit f la fonction définir sur [-1;4] par
1. Calculer la dérivée de la fonction f.
2. Étudier le signe de f'(x).
3. En déduire le sens de variation de f et compléter le tableau de variation ci dessous.
4. Compléter le tableau de valeur suivants.
5. Construire la courbe représentative de f.
IV Cas concret : Optimisation de bénéfices
Exercice 1 : Optimisation des bénéfices.




